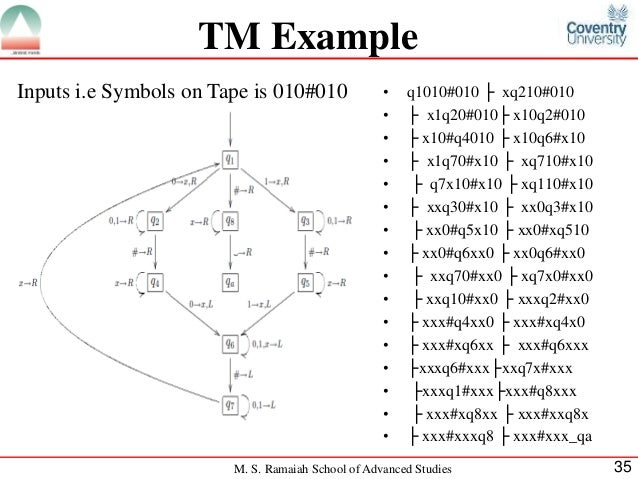
automata Turing Machine calculator - Stack Overflow Mar 27, 2012В В· Turing machines 1. Turing Machines 2. Invented by Alan Turing in 1936.A simple mathematical model of a general purpose computer.It is capable of performing any calculation which can be performed by any computing machine.
Turing Machine What Is a Turing Machine - Make Turing
Automata Theory Introduction Tutorialspoint. Turing Machine Basics: The Turing machine is an invention of a mathematician Alan Turing. Turing machine is a very powerful machine. Any computer problem can be solved through Turing Machine. Just like FA, Turing machine also has some states and some transition. Starting and ending states are also the part of Turing Machine., Turing Machine Introduction - A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type 0 grammars. It was invented in 1936 by Alan T.
In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input to that machine from its own tape. Automata Theory Introduction - The term Automata is derived from the Greek word ГЋВ±ГЎВЅ ГЏ ГЏ ГЋВјГЋВ±ГЏ ГЋВ± which means self-acting. An automaton (Automata in plural) is an abstr
Chapter 5 Turing Machines 138. The language L(M) accepted by the Turing machine is the set of words w context-free languages can be decided by a Turing machine. • Deterministic pushdown automata : the accepted language is decided, except if infinite executions exist (loops with only ε transitions). May 14, 2018 · Turing Machine. Turing Machine was invented by Alan Turing in 1936. It is an accepting device that accept recursively enumerable set of languages generated by type 0 grammars. The Turing machine can be imagined as a finite automaton or control unit equipped with an infinite storage.
Example 3 is a Turing machine that performs some elementary arithmetic. It decides the language ="On input string 1. Scan the input from left to right to be sure that it is a member of ; reject if it is not 2. Return the head at the left-hand end of the tape 3. Cross off an and scan to the right until a If there is any 1 on input tape than machine read 1 and write 0. 3. On state 2, there is a transition of the delta because in the rightmost, always input tape has a delta or can have some other variable instead of the delta. Accept is the final state where machine halts by successfully accepting the string.
Jan 09, 2020 · A Turing machine is a tape with one row of characters and a pointer that can move just one space at a time. The rules for formal languages may grow more and … Theory of Automata: Turing machine Decidablity, Parsing Techniques: Theory of Automata (CS402) Theory of Automata. Lecture N0. 45. Reading Material. Introduction to Computer Theory. Chapter 19. Summary. Turing machine, examples, DELETE subprogram, example, INSERT subprogram, example. Turing machine. The mathematical models (FAs, TGs, PDAs) that
To do this in a Turing Machine is a kind of tedious, because you will need implement the methods of multiply, decrement and comparison. But using unary representation is not so hard to do. Btw, are you using some software to make your tests? In my graduation I use JFLAP, is easy to work with it. Mar 27, 2012В В· Turing machines 1. Turing Machines 2. Invented by Alan Turing in 1936.A simple mathematical model of a general purpose computer.It is capable of performing any calculation which can be performed by any computing machine.
Automata Theory Introduction - The term Automata is derived from the Greek word ГЋВ±ГЎВЅ ГЏ ГЏ ГЋВјГЋВ±ГЏ ГЋВ± which means self-acting. An automaton (Automata in plural) is an abstr Jan 01, 2016В В· How does a tomato differ from a cantaloupe? A PDA can only access the top of its stack, whereas a TM can access any position on an infinite tape. The infinite tape cannot be simulated with a single stack, so a PDA is less computationally powerful
Turing machine as Comparator. Approach for Comparator. Matching two numbers by comparing '1's; Example: 11101111 (3 and 4): compare '1's by marking them 'X' and 'Y' respectively; If '1's are remaining in left of '0' and in right of '0', '1' are finished, then formar is greater Jun 15, 2013 · I The Turing Machine is a theoretical device first described by the British mathematician Alan Turing 1. It is a computing machine that manipulates symbols on a strip of tape. The tape is divided into cells which contain a predefined set of symbols, and is …
May 08, 2013В В· A Turing machine is a theoretical computing machine invented by Alan Turing (1937) to serve as an idealized model for mathematical calculation. A Turing machine consists of a line of cells known What is a Turing machine? A Turing machine is a hypothetical machine thought of by the mathematician Alan Turing in 1936. Despite its simplicity, the machine can simulate ANY computer algorithm, no matter how complicated it is! Above is a very simple representation of a Turing machine.
Turing Machine. Turing machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. There are various features of the Turing machine: It has an external memory which remembers arbitrary long sequence of input. It has unlimited memory capability. A finite state machine is just a set of states and transitions. The only memory it has is what state it is in. Thus, the number of memory states is... finite. A Turing machine is a finite state machine plus a tape memory. Each transition may be a...
Am I correct in saying that we have defined this Turing machine to accept one word at a time, where the words are numbers. We could have made it accept two words, if the algorithm was modified to accept two inputs. Yes, you could produce a Turing machine that decides the language $\{x,y\mid x,y\leq 400\}$. Example of Turing Machine with automata tutorial, finite automata, dfa, nfa, regexp, transition diagram in automata, transition table, theory of automata, examples of dfa, minimization of dfa, non deterministic finite automata, etc.
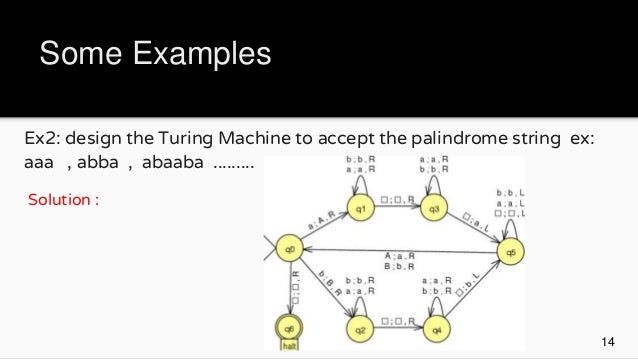
Examples of Turing Machines
automata Turing Machine calculator - Stack Overflow. Encoding Other Automata Using similar techniques, we can encode all the other automata we've seen so far as binary strings. For example, if M is a Turing machine, M refers to a binary encoding of it. More generally, if we have any object O we want to encode as a binary string, we can write it out as O ., Multitape Nondeterministic Turing Machine simulator This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes..
What is the difference between a finite-state machine and. The Turing Machine Informally... TM is essentially a finite automaton that has a single tape of infinite length on which it may read and write data. Advantage of TM over programs as representation of what can be computed: TM is sufficiently simple that we can represent its configuration p recisely, using a simple notation much like ID’s, Encoding Other Automata Using similar techniques, we can encode all the other automata we've seen so far as binary strings. For example, if M is a Turing machine, M refers to a binary encoding of it. More generally, if we have any object O we want to encode as a binary string, we can write it out as O ..
Turing Machine Introduction Tutorialspoint
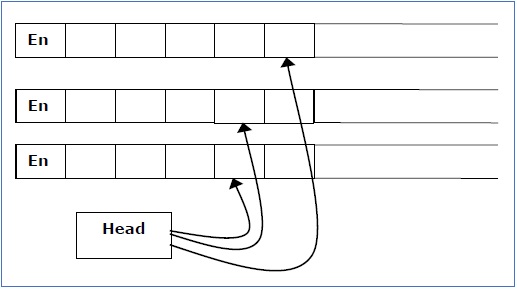
Turing Machine for complement of a string in Theory Of. The Turing Machine Informally... TM is essentially a finite automaton that has a single tape of infinite length on which it may read and write data. Advantage of TM over programs as representation of what can be computed: TM is sufficiently simple that we can represent its configuration p recisely, using a simple notation much like ID’s https://en.m.wikipedia.org/wiki/Post%E2%80%93Turing_machine Jan 01, 2016 · How does a tomato differ from a cantaloupe? A PDA can only access the top of its stack, whereas a TM can access any position on an infinite tape. The infinite tape cannot be simulated with a single stack, so a PDA is less computationally powerful.
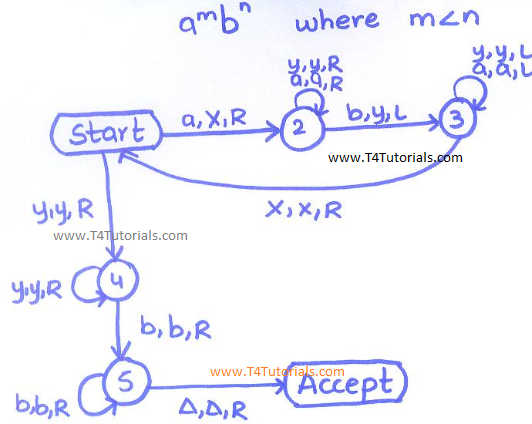
Can someone give me a code of example for Turing Machine Calculator which can accept these inputs 30+25x3-2/5= and the output is 104.6 this calculator cant accept these input 3+52-2 43+1=12 0... May 23, 2013 · Turing Machines and Finite Automata: The Basic Distinctions. The capabilities of Turing Machines, Universal Turing Machines, and finite automata are easily confused, and usage outside the specialist literature doesn’t help. Of the three, Universal Turing Machines are the most powerful. The Universal Turing Machine was originally described
Multitape Nondeterministic Turing Machine simulator This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes. Example 3 is a Turing machine that performs some elementary arithmetic. It decides the language ="On input string 1. Scan the input from left to right to be sure that it is a member of ; reject if it is not 2. Return the head at the left-hand end of the tape 3. Cross off an and scan to the right until a
May 14, 2018 · Turing Machine. Turing Machine was invented by Alan Turing in 1936. It is an accepting device that accept recursively enumerable set of languages generated by type 0 grammars. The Turing machine can be imagined as a finite automaton or control unit equipped with an infinite storage. The Turing Machine Informally... TM is essentially a finite automaton that has a single tape of infinite length on which it may read and write data. Advantage of TM over programs as representation of what can be computed: TM is sufficiently simple that we can represent its configuration p recisely, using a simple notation much like ID’s
Prerequisite – Turing Machine A problem is said to be Decidable if we can always construct a corresponding algorithm that can answer the problem correctly. We can intuitively understand Decidable problems by considering a simple example. Suppose we are asked to compute all the prime numbers in the range of 1000 to 2000. Mar 27, 2012 · Turing machines 1. Turing Machines 2. Invented by Alan Turing in 1936.A simple mathematical model of a general purpose computer.It is capable of performing any calculation which can be performed by any computing machine.
Finite state automata No Machine Pushdown automata Yes Linear bounded automata Unknown Turing machine No 23 Summary Abstract machines are foundation of all modern computers. Simple computational models are easier to understand. Leads to deeper understanding of computation. Goal: simplest machine "as powerful" as conventional computers. Turing machine as Comparator. Approach for Comparator. Matching two numbers by comparing '1's; Example: 11101111 (3 and 4): compare '1's by marking them 'X' and 'Y' respectively; If '1's are remaining in left of '0' and in right of '0', '1' are finished, then formar is greater
The most general and powerful automata is the Turing machine. The major objective of automata theory is to develop methods by which computer scientists can describe and analyze the dynamic behavior of discrete systems, in which signals are sampled periodically. The behavior of these discrete systems is determined by the way that the system is A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L. For example the Turing machine of Example 1 above goes through the following sequence of configurations to accept the string aba: ( q 0, aba ) ( q 1, aba ) ( q 2, aba ) ( q 3, aba
May 14, 2018В В· Turing Machine. Turing Machine was invented by Alan Turing in 1936. It is an accepting device that accept recursively enumerable set of languages generated by type 0 grammars. The Turing machine can be imagined as a finite automaton or control unit equipped with an infinite storage. The Turing Machine A Turing machine consists of three parts: A finite-state control that issues commands, an infinite tape for input and scratch space, and a tape head that can read and write a single tape cell. At each step, the Turing machine writes a symbol to the tape cell under the tape head, changes state, and moves the tape head to the left or to the right.
A Turing machine is a mathematical model of computation that defines an abstract machine, which manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, given any computer algorithm, a Turing machine capable of simulating that algorithm's logic can be constructed.. The machine operates on an infinite memory tape divided into discrete "cells". Multitape Nondeterministic Turing Machine simulator This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes.
In this Turing machine example, you can see the machine following a simple set of steps to count in binary. How the Turing Machine Counts. Counting is really just repeatedly adding one to a number. If we count in decimal like most humans do, we keep adding one to a number. Turing Machine Introduction - A Turing Machine is an accepting device which accepts the languages (recursively enumerable set) generated by type 0 grammars. It was invented in 1936 by Alan T
Apr 01, 2019 · Turing didn’t come up with a machine. Turing came up with an abstract model for all machines. In other words, any algorithm ever can be built on a … Turing machine as Comparator. Approach for Comparator. Matching two numbers by comparing '1's; Example: 11101111 (3 and 4): compare '1's by marking them 'X' and 'Y' respectively; If '1's are remaining in left of '0' and in right of '0', '1' are finished, then formar is greater
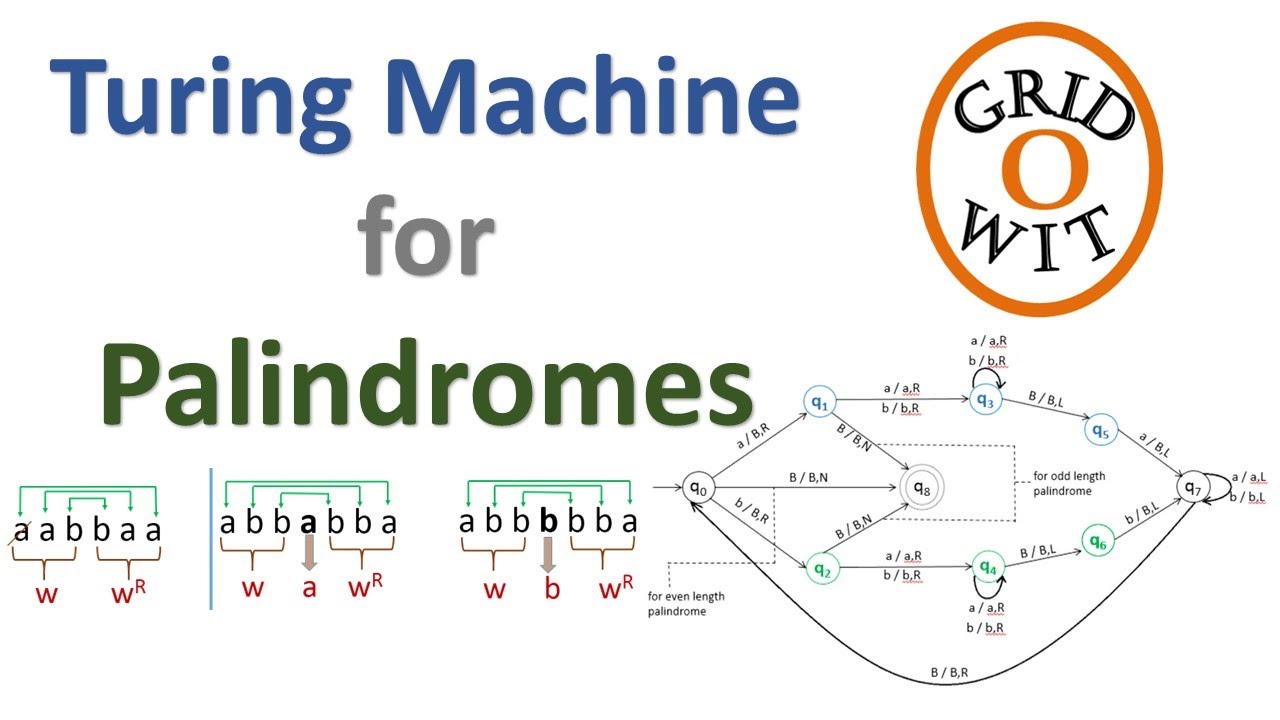
Multitape Nondeterministic Turing Machine simulator This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes. Example 3 is a Turing machine that performs some elementary arithmetic. It decides the language ="On input string 1. Scan the input from left to right to be sure that it is a member of ; reject if it is not 2. Return the head at the left-hand end of the tape 3. Cross off an and scan to the right until a
Turing Machines Computer Science
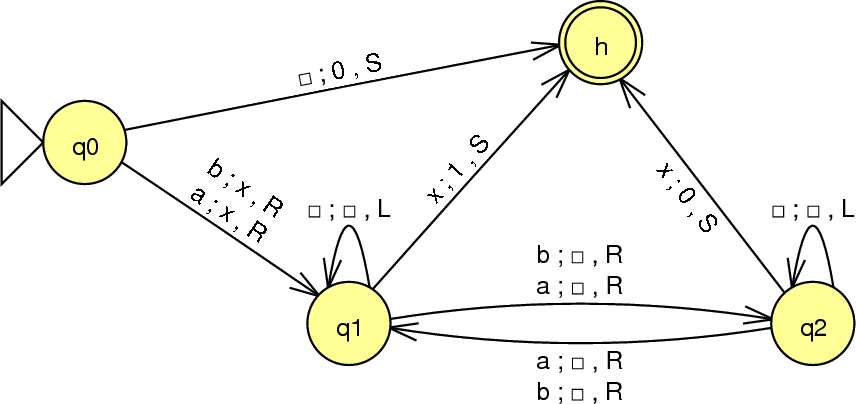
The Universal Turing Machine. Theory of Automata: Turing machine Decidablity, Parsing Techniques: Theory of Automata (CS402) Theory of Automata. Lecture N0. 45. Reading Material. Introduction to Computer Theory. Chapter 19. Summary. Turing machine, examples, DELETE subprogram, example, INSERT subprogram, example. Turing machine. The mathematical models (FAs, TGs, PDAs) that, Theory of Computation The most used computational model is the Turing machine and it's an example of the theory of automata. A Turing machine is a machine that helps solve problems, using a tape that has no more than repeated units of (1), (0), and (). It is believed a Turing machine can do more than an actual computer..
Turing machine in Automata Part 1 - YouTube
Turing Machines cs.odu.edu. Automata Theory Introduction - The term Automata is derived from the Greek word Î±á½ Ï Ï Î¼Î±Ï Î± which means self-acting. An automaton (Automata in plural) is an abstr, Turing Machine Extensions In fact, there are lots of extensions we can make to our basic Turing machine model. They may make it easier to write Turing machine programs, but none of them increase the power of the Turing machine because: We can show that every extended machine has ….
Jun 15, 2013 · I The Turing Machine is a theoretical device first described by the British mathematician Alan Turing 1. It is a computing machine that manipulates symbols on a strip of tape. The tape is divided into cells which contain a predefined set of symbols, and is … Multitape Nondeterministic Turing Machine simulator This article tackles both theoretical and practical issues in Computer Science (CS). It reviews Turing Machines (TMs), a fundamental class of automata and presents a simulator for a broad variant of TMs: nondeterministic with multiple tapes.
Example of Turing Machine with automata tutorial, finite automata, dfa, nfa, regexp, transition diagram in automata, transition table, theory of automata, examples of dfa, minimization of dfa, non deterministic finite automata, etc. May 23, 2013 · Turing Machines and Finite Automata: The Basic Distinctions. The capabilities of Turing Machines, Universal Turing Machines, and finite automata are easily confused, and usage outside the specialist literature doesn’t help. Of the three, Universal Turing Machines are the most powerful. The Universal Turing Machine was originally described
Turing Machine Basics: The Turing machine is an invention of a mathematician Alan Turing. Turing machine is a very powerful machine. Any computer problem can be solved through Turing Machine. Just like FA, Turing machine also has some states and some transition. Starting and ending states are also the part of Turing Machine. Mar 27, 2012В В· Turing machines 1. Turing Machines 2. Invented by Alan Turing in 1936.A simple mathematical model of a general purpose computer.It is capable of performing any calculation which can be performed by any computing machine.
Turing Machine. Turing machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. There are various features of the Turing machine: It has an external memory which remembers arbitrary long sequence of input. It has unlimited memory capability. Turing Machine Basics: The Turing machine is an invention of a mathematician Alan Turing. Turing machine is a very powerful machine. Any computer problem can be solved through Turing Machine. Just like FA, Turing machine also has some states and some transition. Starting and ending states are also the part of Turing Machine.
The first 4 programs are found from this website and are very good demonstrations of what a 3-symbol Turing machine can do.. Binary Counter. This program reads the current binary number printed on the tape and increments it by 1 before stopping. Turing Machine Basics: The Turing machine is an invention of a mathematician Alan Turing. Turing machine is a very powerful machine. Any computer problem can be solved through Turing Machine. Just like FA, Turing machine also has some states and some transition. Starting and ending states are also the part of Turing Machine.
May 23, 2013 · Turing Machines and Finite Automata: The Basic Distinctions. The capabilities of Turing Machines, Universal Turing Machines, and finite automata are easily confused, and usage outside the specialist literature doesn’t help. Of the three, Universal Turing Machines are the most powerful. The Universal Turing Machine was originally described The Turing Machine Informally... TM is essentially a finite automaton that has a single tape of infinite length on which it may read and write data. Advantage of TM over programs as representation of what can be computed: TM is sufficiently simple that we can represent its configuration p recisely, using a simple notation much like ID’s
Operation. A linear bounded automaton is a nondeterministic Turing machine that satisfies the following three conditions: . Its input alphabet includes two special symbols, serving as left and right endmarkers. Its transitions may not print other symbols over the endmarkers. A deterministic Turing machine, on the other hand, can not guess the midpoint of the string x. It must find the midpoint by for example pairing off symbols from either end of x. Formally a nondeterministic Turing machine is a Turing machine whose transition function takes values that are subsets of ( Q { h } ) ( {} { R , …
Theory of Computation The most used computational model is the Turing machine and it's an example of the theory of automata. A Turing machine is a machine that helps solve problems, using a tape that has no more than repeated units of (1), (0), and (). It is believed a Turing machine can do more than an actual computer. Jan 01, 2016В В· How does a tomato differ from a cantaloupe? A PDA can only access the top of its stack, whereas a TM can access any position on an infinite tape. The infinite tape cannot be simulated with a single stack, so a PDA is less computationally powerful
Turing Machines: Questions Examine the formal de nition of a Turing machine to answer the following questions, and explain your reasoning. 1.Can a Turing machine ever write the blank symbol ton its tape? 2.Can the tape alphabet be the same as the input alphabet ? 3.Can a Turing machine’s head ever be in the same location in two successive steps? Finite state automata No Machine Pushdown automata Yes Linear bounded automata Unknown Turing machine No 23 Summary Abstract machines are foundation of all modern computers. Simple computational models are easier to understand. Leads to deeper understanding of computation. Goal: simplest machine "as powerful" as conventional computers.
In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input to that machine from its own tape. A finite state machine is just a set of states and transitions. The only memory it has is what state it is in. Thus, the number of memory states is... finite. A Turing machine is a finite state machine plus a tape memory. Each transition may be a...
Turing’s Machine A Simple Example – the logic grimoire
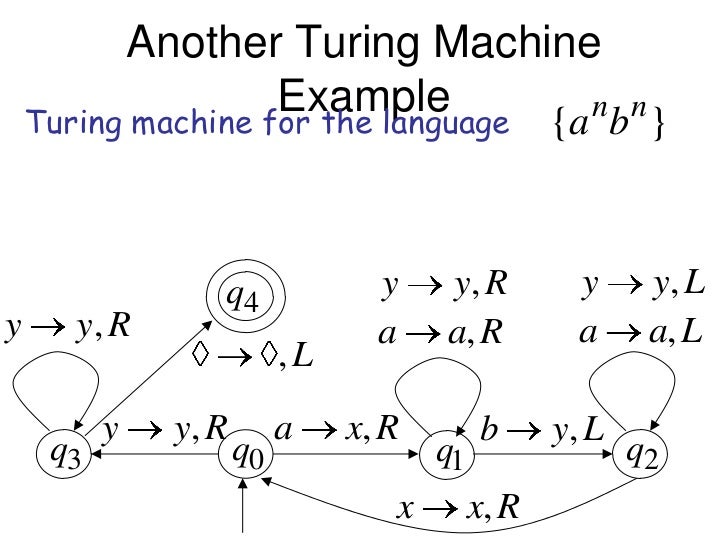
Questions about Turing Machine Computer Science Stack. Anything that can be computed by a real computer can also be computed by a Turing machine. A Turing machine, for example can simulate any type of functions used in programming language. Recursion and parameter passing are some typical examples. A Turing machine can also be used to simplify the statements of an algorithm., Mar 27, 2012В В· Turing machines 1. Turing Machines 2. Invented by Alan Turing in 1936.A simple mathematical model of a general purpose computer.It is capable of performing any calculation which can be performed by any computing machine..
What is a Turing machine? Department of Computer Science. Finite state automata No Machine Pushdown automata Yes Linear bounded automata Unknown Turing machine No 23 Summary Abstract machines are foundation of all modern computers. Simple computational models are easier to understand. Leads to deeper understanding of computation. Goal: simplest machine "as powerful" as conventional computers., Turing Machines: Questions Examine the formal de nition of a Turing machine to answer the following questions, and explain your reasoning. 1.Can a Turing machine ever write the blank symbol ton its tape? 2.Can the tape alphabet be the same as the input alphabet ? 3.Can a Turing machine’s head ever be in the same location in two successive steps?.
Turing machine as Comparator Scanftree.com
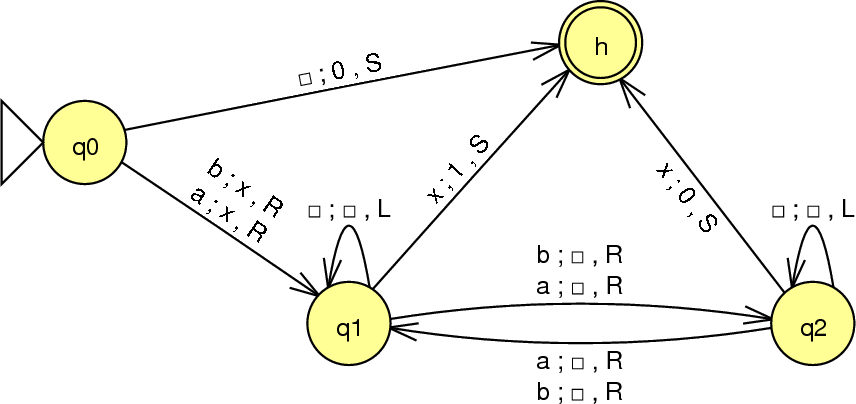
Decidable and Undecidable problems in Theory of. A deterministic Turing machine, on the other hand, can not guess the midpoint of the string x. It must find the midpoint by for example pairing off symbols from either end of x. Formally a nondeterministic Turing machine is a Turing machine whose transition function takes values that are subsets of ( Q { h } ) ( {} { R , … https://en.wikipedia.org/wiki/Turing_machine_examples Turing Machine. Turing machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. There are various features of the Turing machine: It has an external memory which remembers arbitrary long sequence of input. It has unlimited memory capability..
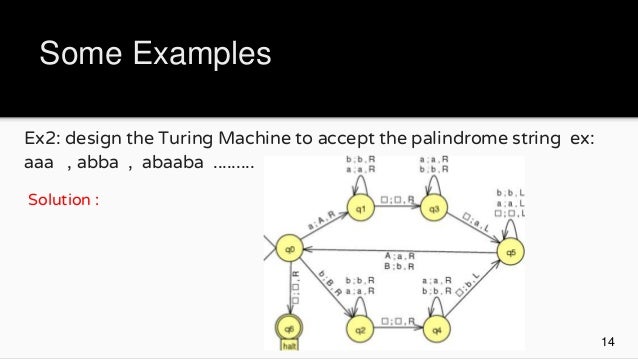
Jun 15, 2013 · I The Turing Machine is a theoretical device first described by the British mathematician Alan Turing 1. It is a computing machine that manipulates symbols on a strip of tape. The tape is divided into cells which contain a predefined set of symbols, and is … May 14, 2018 · Turing Machine. Turing Machine was invented by Alan Turing in 1936. It is an accepting device that accept recursively enumerable set of languages generated by type 0 grammars. The Turing machine can be imagined as a finite automaton or control unit equipped with an infinite storage.
Finite state automata No Machine Pushdown automata Yes Linear bounded automata Unknown Turing machine No 23 Summary Abstract machines are foundation of all modern computers. Simple computational models are easier to understand. Leads to deeper understanding of computation. Goal: simplest machine "as powerful" as conventional computers. Prerequisite – Turing Machine A problem is said to be Decidable if we can always construct a corresponding algorithm that can answer the problem correctly. We can intuitively understand Decidable problems by considering a simple example. Suppose we are asked to compute all the prime numbers in the range of 1000 to 2000.
In computer science, a universal Turing machine (UTM) is a Turing machine that can simulate an arbitrary Turing machine on arbitrary input. The universal machine essentially achieves this by reading both the description of the machine to be simulated as well as the input to that machine from its own tape. A Turing machine is a mathematical model of computation that defines an abstract machine, which manipulates symbols on a strip of tape according to a table of rules. Despite the model's simplicity, given any computer algorithm, a Turing machine capable of simulating that algorithm's logic can be constructed.. The machine operates on an infinite memory tape divided into discrete "cells".
Jan 09, 2020 · A Turing machine is a tape with one row of characters and a pointer that can move just one space at a time. The rules for formal languages may grow more and … Turing Machine. Turing machine was invented in 1936 by Alan Turing. It is an accepting device which accepts Recursive Enumerable Language generated by type 0 grammar. There are various features of the Turing machine: It has an external memory which remembers arbitrary long sequence of input. It has unlimited memory capability.
Chapter 5 Turing Machines 138. The language L(M) accepted by the Turing machine is the set of words w context-free languages can be decided by a Turing machine. • Deterministic pushdown automata : the accepted language is decided, except if infinite executions exist (loops with only ε transitions). A Turing machine T is said to decide a language L if and only if T writes "yes" and halts if a string is in L and T writes "no" and halts if a string is not in L. For example the Turing machine of Example 1 above goes through the following sequence of configurations to accept the string aba: ( q 0, aba ) ( q 1, aba ) ( q 2, aba ) ( q 3, aba
A language is Turing recognizable or r.e if there is a Turing machine accepting it. Turing decidable or recursive A language is decidable (or recursive) if there is a Turing machine accepting it, which has the additional property that it halts on all possible inputs. Every decidable language is Turing recognizable, but is the converse true? Automata theory is the study of abstract machines and automata, as well as the computational problems that can be solved using them. It is a theory in theoretical computer science and discrete mathematics (a subject of study in both mathematics and computer science).The word automata (the plural of automaton) comes from the Greek word О±бЅђП„ПЊОјО±П„О±, which means "self-making".
Finite state automata No Machine Pushdown automata Yes Linear bounded automata Unknown Turing machine No 23 Summary Abstract machines are foundation of all modern computers. Simple computational models are easier to understand. Leads to deeper understanding of computation. Goal: simplest machine "as powerful" as conventional computers. Prerequisite – Turing Machine A problem is said to be Decidable if we can always construct a corresponding algorithm that can answer the problem correctly. We can intuitively understand Decidable problems by considering a simple example. Suppose we are asked to compute all the prime numbers in the range of 1000 to 2000.
A deterministic Turing machine, on the other hand, can not guess the midpoint of the string x. It must find the midpoint by for example pairing off symbols from either end of x. Formally a nondeterministic Turing machine is a Turing machine whose transition function takes values that are subsets of ( Q { h } ) ( {} { R , … To do this in a Turing Machine is a kind of tedious, because you will need implement the methods of multiply, decrement and comparison. But using unary representation is not so hard to do. Btw, are you using some software to make your tests? In my graduation I use JFLAP, is easy to work with it.
What is a Turing machine? A Turing machine is a hypothetical machine thought of by the mathematician Alan Turing in 1936. Despite its simplicity, the machine can simulate ANY computer algorithm, no matter how complicated it is! Above is a very simple representation of a Turing machine. Turing machine Introduction. Till now we have seen machines which can move in one direction: left to right. But Turing machine can move in both directions and also it …
A language is Turing recognizable or r.e if there is a Turing machine accepting it. Turing decidable or recursive A language is decidable (or recursive) if there is a Turing machine accepting it, which has the additional property that it halts on all possible inputs. Every decidable language is Turing recognizable, but is the converse true? May 08, 2013В В· A Turing machine is a theoretical computing machine invented by Alan Turing (1937) to serve as an idealized model for mathematical calculation. A Turing machine consists of a line of cells known

Apr 01, 2019 · Turing didn’t come up with a machine. Turing came up with an abstract model for all machines. In other words, any algorithm ever can be built on a … Turing machine as Comparator. Approach for Comparator. Matching two numbers by comparing '1's; Example: 11101111 (3 and 4): compare '1's by marking them 'X' and 'Y' respectively; If '1's are remaining in left of '0' and in right of '0', '1' are finished, then formar is greater


