List of np complete problems pdf Rutherford

ON THE CLASSIFICATION OF NP COMPLETE PROBLEMS AND However, David Zuckerman showed in 1996 that every one of these 21 problems has a constrained optimization version that is impossible to approximate within any constant factor unless P = NP, by showing that Karp's approach to reduction generalizes to a specific type of approximability reduction.
16 NP-Hard Problems (December 3 and 5) uniba.sk
Statement of the Problem. 16 NP-Hard Problems (December 3 and 5) 16.1 ‘E cient’ Problems A long time ago1, theoretical computer scientists like Steve Cook and Dick Karp decided that a minimum requirement of any e cient algorithm is that it runs in polynomial time: O(nc) for some constant c. People recognized early on that not all problems can be solved this quickly, NP problems have their own significance in programming, but the discussion becomes quite hot when we deal with differences between NP, P , NP-Complete and NP-hard. P and NP- Many of us know the difference between them. P- Polynomial time solving. Problems ….
NP-Completeness How would you define NP-Complete? They are the “hardest” problems in NP Definition of NP-Complete Q is an NP-Complete problem if: 1) Q is in NP 2) every other NP problem polynomial time reducible to Q Getting Started How do you show that EVERY NP problem reduces to Q? One way would be to already have an NP-Complete problem NP-Hard and NP-Complete Problems 2 – The problems in class NPcan be verified in polynomial time If we are given a certificate of a solution, we can verify that …
However, David Zuckerman showed in 1996 that every one of these 21 problems has a constrained optimization version that is impossible to approximate within any constant factor unless P = NP, by showing that Karp's approach to reduction generalizes to a specific type of approximability reduction. P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for
NP-Complete: can be solved in Polynomial time only using a Non-deterministic method. NP-Complete may not last. Oh, one more thing, it is believed that if anyone could *ever* solve an "NP-Complete" problem in "P" time, then *all* "NP-complete" problems could also be solved that way by using the same method, and the whole class of "NP-Complete List of PSPACE-complete problems. Jump to navigation Jump to search Here are some of the more commonly known problems that are PSPACE-complete when expressed as decision problems. This list is in no way comprehensive.
NP Certification algorithm intuition. ・Certifier views things from "managerial" viewpoint. ・Certifier doesn't determine whether s ∈ X on its own; rather, it checks a proposed proof t that s ∈ X. Def. Algorithm C(s, t) is a certifier for problem X if for every string s, s ∈ X iff there exists a string t such that C(s, t) = yes. Def. NP is the set of problems for which there exists a LECTURE NOTES: NP-COMPLETE PROBLEMS 3 checked in polynomial time. W is known as the ”witness” or ”certificate.” At worst, all solutions w must be checked, giving exponential running time.
Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness. In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete.In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the boolean satisfiability problem is NP-complete (also called the Cook-Levin theorem) to show that there is a polynomial time many-one reduction from …
4 NP –HARD AND NP –COMPLETE PROBLEMS BASIC CONCEPTS •The computing times of algorithms fall into two groups. •Group1–consists of problems whose solutions are bounded by … Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness.
Adiabatic quantum optimization fails for random instances of NP-complete problems Boris Altshuler,1,2, Hari Krovi, 2,yand Jeremie Roland z 1Columbia University 2NEC Laboratories America Inc Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem
P, NP, and NP-Completeness The Basics of Computational Complexity The focus of this book is the P versus NP Question and the theory of NP-completeness. It also provides adequate preliminaries regarding computational problems and compu-tational models. The P versus NP Question asks whether finding solutions is harder than checking Most Tensor Problems Are NP-Hard CHRISTOPHER J. HILLAR, Mathematical Sciences Research Institute LEK-HENG LIM, University of Chicago We prove that multilinear (tensor) analogues of many efficiently computable problems in numerical linear algebra are NP-hard. Our list includes: determining the feasibility of a system of bilinear equations, de-
Some First NP-complete problem We need to nd some rst NP-complete problem. Finding the rst NP-complete problem was the result of the Cook-Levin theorem. We’ll deal with this later. For now, trust me that: Independent Set is a packing problem and is NP-complete. Vertex Cover is a covering problem and is NP-complete. NP-complete problems are closely related to each other and all can be reduced to each other in polynomial time. (Of course, not all such reductions are efficient.) In this work we focus on four canonical NP-hard problems [23]. Maximal Independent Set (MIS). Given an undirected graph, find the largest subset of vertices in
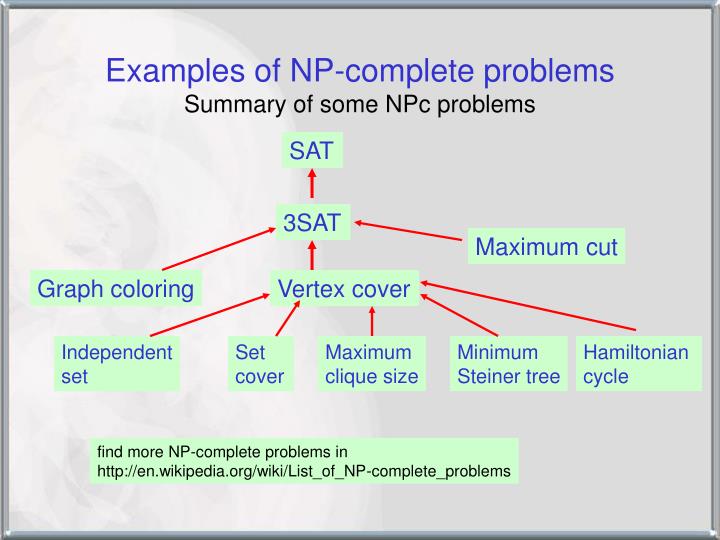
Computer Algorithms Design and Analysis Known NP-Complete Problem Garey & Johnson: Computer and Intractability: A Guide to the Theory of NP-Completeness, Freeman, 1979 About 300 problems i.e. SAT, Clique, Hamiltonian, Partition, Knapsack … Note: 0-1 knapsack problem is NPC problem, but it can be solved by using dynamic programming in polynomial time, think about why and • NP-complete problems are always yes/no questions. • In practice, we tend to want to solve optimization problems, where our task is to minimize (or maximize) a function, f(x), of the input, x. • Optimization problems, strictly speaking, can’t be NP-complete (only NP-hard).
16 NP-Hard Problems (December 3 and 5) uniba.sk

CMSC 451 Reductions & NP-completeness. Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem, LECTURE NOTES: NP-COMPLETE PROBLEMS 3 checked in polynomial time. W is known as the ”witness” or ”certificate.” At worst, all solutions w must be checked, giving exponential running time..

Problème NP-complet — Wikipédia
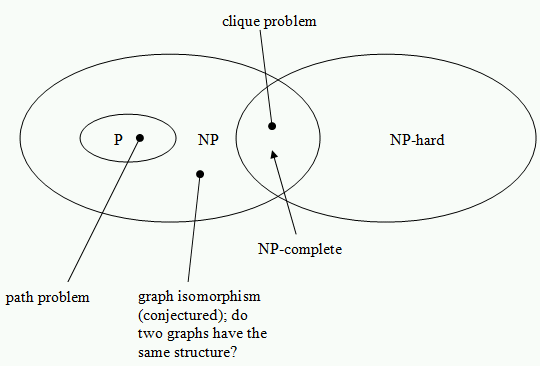
NP hard and NP Complete problems Basic Concepts. An important notion in this context is the set of NP-complete decision problems, which is a subset of NP and might be informally described as the "hardest" problems in NP. If there is a polynomial-time algorithm for even one of them, then there is a polynomial-time algorithm for all the problems in NP. https://en.wikipedia.org/wiki/P_(complexity) Most Tensor Problems Are NP-Hard CHRISTOPHER J. HILLAR, Mathematical Sciences Research Institute LEK-HENG LIM, University of Chicago We prove that multilinear (tensor) analogues of many efficiently computable problems in numerical linear algebra are NP-hard. Our list includes: determining the feasibility of a system of bilinear equations, de-.

THE P VERSUS NP PROBLEM STEPHEN COOK 1. Statement of the Problem The P versus NP problem is to determine whether every language accepted by some nondeterministic algorithm in polynomial time is also accepted by some (deterministic) algorithm in polynomial time. To define the problem precisely it is necessary to give a formal model of a NP problems have their own significance in programming, but the discussion becomes quite hot when we deal with differences between NP, P , NP-Complete and NP-hard. P and NP- Many of us know the difference between them. P- Polynomial time solving. Problems …
NP-complete problems off all shapes and colors. •These are universal NP-problems...if you can solve them efficiently, you can solve ANY problem in NP efficiently. •L is NP-complete if: –L is in NP –ANY other problem in NP reduces to L. •If you come up with an efficient algorithm to 3-color a map, then P=NP. In computational complexity theory, Karp's 21 NP-complete problems are a set of computational problems which are NP-complete.In his 1972 paper, "Reducibility Among Combinatorial Problems", Richard Karp used Stephen Cook's 1971 theorem that the boolean satisfiability problem is NP-complete (also called the Cook-Levin theorem) to show that there is a polynomial time many-one reduction from …
Most Tensor Problems Are NP-Hard CHRISTOPHER J. HILLAR, Mathematical Sciences Research Institute LEK-HENG LIM, University of Chicago We prove that multilinear (tensor) analogues of many efficiently computable problems in numerical linear algebra are NP-hard. Our list includes: determining the feasibility of a system of bilinear equations, de- Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness.
List of PSPACE-complete problems. Jump to navigation Jump to search Here are some of the more commonly known problems that are PSPACE-complete when expressed as decision problems. This list is in no way comprehensive. Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem
Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness. Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem
Class NP, NP-complete, and NP-hard problems W. H¨am¨al¨ainen November 6, 2006 1 Class NP Class NP contains all computational problems such that the corre- sponding decision problem can be solved in a polynomial time by a nondeterministic Turing machine. P, NP, and NP-Completeness The Basics of Computational Complexity The focus of this book is the P versus NP Question and the theory of NP-completeness. It also provides adequate preliminaries regarding computational problems and compu-tational models. The P versus NP Question asks whether finding solutions is harder than checking
LECTURE NOTES: NP-COMPLETE PROBLEMS 3 checked in polynomial time. W is known as the ”witness” or ”certificate.” At worst, all solutions w must be checked, giving exponential running time. List of PSPACE-complete problems. Jump to navigation Jump to search Here are some of the more commonly known problems that are PSPACE-complete when expressed as decision problems. This list is in no way comprehensive.
An important notion in this context is the set of NP-complete decision problems, which is a subset of NP and might be informally described as the "hardest" problems in NP. If there is a polynomial-time algorithm for even one of them, then there is a polynomial-time algorithm for all the problems in NP. On dit qu’un problème de décision est « NP-complet » lorsque le langage correspondant est NP-complet. C’est une notion informelle car il existe plusieurs moyens de coder les instances d’un problème, mais cela ne pose pas de difficultés dans la mesure où on emploie un codage raisonnable du problème vers le langage considéré (voir la section NP-complétude faible).
THE P VERSUS NP PROBLEM STEPHEN COOK 1. Statement of the Problem The P versus NP problem is to determine whether every language accepted by some nondeterministic algorithm in polynomial time is also accepted by some (deterministic) algorithm in polynomial time. To define the problem precisely it is necessary to give a formal model of a Clearly, all problems in P are also in NP, so P NP. NP-Complete problems are in a formal sense the hardest problems in NP|if any one of them can be solved in poly time, then they can all be solved in poly time; this would result in the set equality P = NP. Similarly, if any one of the NP-Complete problem can be shown to require exponential
2.Select a problem Z known to be NP-Complete. 3.Consider an arbitrary instance s Z of problem Z. Show how to construct, in polynomial time, an instance s X of problem X such that (a)If s Z 2 Z, then s X 2 X and (b)If s X 2 X, then sz 2 z. T. M. Murali December 2, 2009 CS 4104: NP-complete problems NP-complete problems are the hardest in NP: if any NP-complete problem is p-time solvable, then all problems in NP are p-time solvable How to formally compare easiness/hardness of problems? Reductions Reduce language L 1 to L 2 via function f: 1. Convert input x of L 1 to instance f(x) of L 2 2. Apply decision algorithm for L 2 to f(x) Running time = time to compute f + time to apply decision
Although I think "List of NP-complete problems" is an excellent article (especially as a source of new articles to write), I'm concerned that we may also be vulnerable to claims of copyright violation because we essentially steal the NP Guide's presentation. The Partition-Knapsack Problem This problem is what we originally referred to as “knapsack.” Given a list of integers L, can we partition it into two disjoint sets whose sums are equal? Example: L={3,4,5,6,14,18}, Solution: 3+4+18=5+6+16 Partition-Knapsack is NP-complete; reduction from Knapsack.
NP-complete problems web.cse.msstate.edu

NP-complete problems web.cse.msstate.edu. P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for, NP-complete problem, any of a class of computational problems for which no efficient solution algorithm has been found. Many significant computer-science problems belong to this class—e.g., the traveling salesman problem, satisfiability problems, and graph-covering problems. So-called easy, or.
More NP-Complete Problems Stanford University
NP-Completeness. P, NP, and NP-Completeness The Basics of Computational Complexity The focus of this book is the P versus NP Question and the theory of NP-completeness. It also provides adequate preliminaries regarding computational problems and compu-tational models. The P versus NP Question asks whether finding solutions is harder than checking, THE P VERSUS NP PROBLEM STEPHEN COOK 1. Statement of the Problem The P versus NP problem is to determine whether every language accepted by some nondeterministic algorithm in polynomial time is also accepted by some (deterministic) algorithm in polynomial time. To define the problem precisely it is necessary to give a formal model of a.
Although I think "List of NP-complete problems" is an excellent article (especially as a source of new articles to write), I'm concerned that we may also be vulnerable to claims of copyright violation because we essentially steal the NP Guide's presentation. NP-complete Problems and Physical Reality Scott Aaronson∗ Abstract Can NP-complete problems be solved efficiently in the physical universe? I survey proposals including soap bubbles, protein folding, quantum computing, quantum advice, quantum adia-batic algorithms, quantum-mechanical nonlinearities, hidden variables, relativistic time dilation,
2.Select a problem Z known to be NP-Complete. 3.Consider an arbitrary instance s Z of problem Z. Show how to construct, in polynomial time, an instance s X of problem X such that (a)If s Z 2 Z, then s X 2 X and (b)If s X 2 X, then sz 2 z. T. M. Murali December 2, 2009 CS 4104: NP-complete problems P, NP, and NP-Completeness The Basics of Computational Complexity The focus of this book is the P versus NP Question and the theory of NP-completeness. It also provides adequate preliminaries regarding computational problems and compu-tational models. The P versus NP Question asks whether finding solutions is harder than checking
Some First NP-complete problem We need to nd some rst NP-complete problem. Finding the rst NP-complete problem was the result of the Cook-Levin theorem. We’ll deal with this later. For now, trust me that: Independent Set is a packing problem and is NP-complete. Vertex Cover is a covering problem and is NP-complete. NP-hard problem. Deciding if a graph have a MIS of size k, deciding if a subset is a MIS, are NP-complete problems (this is typically proven via a reduction to SAT). This problem was one of Richard Karp’s original 21 problems shown NP-complete in his 1972 seminal article [34].
P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem
Or trying giving `NP-complete' or `NP and complete' as a search term to http://liinwww.ira.uka.de/searchbib/index> (This is basically a bibliography database, but, you can click on the `on-line papers' button to list electronically readable full texts). NP-Complete: can be solved in Polynomial time only using a Non-deterministic method. NP-Complete may not last. Oh, one more thing, it is believed that if anyone could *ever* solve an "NP-Complete" problem in "P" time, then *all* "NP-complete" problems could also be solved that way by using the same method, and the whole class of "NP-Complete
On dit qu’un problème de décision est « NP-complet » lorsque le langage correspondant est NP-complet. C’est une notion informelle car il existe plusieurs moyens de coder les instances d’un problème, mais cela ne pose pas de difficultés dans la mesure où on emploie un codage raisonnable du problème vers le langage considéré (voir la section NP-complétude faible). NP-complete problem, any of a class of computational problems for which no efficient solution algorithm has been found. Many significant computer-science problems belong to this class—e.g., the traveling salesman problem, satisfiability problems, and graph-covering problems. So-called easy, or
NP-Complete: can be solved in Polynomial time only using a Non-deterministic method. NP-Complete may not last. Oh, one more thing, it is believed that if anyone could *ever* solve an "NP-Complete" problem in "P" time, then *all* "NP-complete" problems could also be solved that way by using the same method, and the whole class of "NP-Complete An important notion in this context is the set of NP-complete decision problems, which is a subset of NP and might be informally described as the "hardest" problems in NP. If there is a polynomial-time algorithm for even one of them, then there is a polynomial-time algorithm for all the problems in NP.
On dit qu’un problème de décision est « NP-complet » lorsque le langage correspondant est NP-complet. C’est une notion informelle car il existe plusieurs moyens de coder les instances d’un problème, mais cela ne pose pas de difficultés dans la mesure où on emploie un codage raisonnable du problème vers le langage considéré (voir la section NP-complétude faible). Connecting problems together. NP-Completeness What are the hardest problems in NP? The Cook-Levin Theorem A concrete NP-complete problem. Recap from Last Time. The Limits of Computability RE A HALT TM L D co-RE R ADD 0*1* A HALT TM L D EQ TM EQ TM. The Limits of Efficient Computation P NP R. P and NP Refresher The class P consists of all problems solvable in deterministic polynomial time. …
algorithm, then P = NP. If any problem in NP cannot be solved by a polynomial-time deterministic algorithm, then NP-complete problems are not in P. • This theorem makes NP-complete problems the focus of the P=NP question. • Most theoretical computer scientists believe that P ≠ NP. But no one has proved this yet. NP P NP P NP-complete NP A Some NP-Complete Problems To ask the hard question is simple. But what does it mean? What are we going to do? W. H. Auden In this appendix we present a brief list of NP-complete problems; we restrict
22/08/2013 · NP-complete problems are the hardest problems in NP set. A decision problem L is NP-complete if: 1) L is in NP (Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution). 2) Every problem in NP … However, David Zuckerman showed in 1996 that every one of these 21 problems has a constrained optimization version that is impossible to approximate within any constant factor unless P = NP, by showing that Karp's approach to reduction generalizes to a specific type of approximability reduction.
Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness. NP problems have their own significance in programming, but the discussion becomes quite hot when we deal with differences between NP, P , NP-Complete and NP-hard. P and NP- Many of us know the difference between them. P- Polynomial time solving. Problems …
LECTURE NOTES NP-COMPLETE PROBLEMS

NP-Complete Problems Virginia Tech. NP Complete (abbreviated as NPC) problems, standing at the crux of deciding whether P=NP, are among hardest problems in computer science and other related areas. Through decades, NPC problems are treated as one class. Observing that NPC problems have different natures, it is unlikely that they will have the same complexity. Our intensive study shows that NPC problems are not all equivalent in, However, David Zuckerman showed in 1996 that every one of these 21 problems has a constrained optimization version that is impossible to approximate within any constant factor unless P = NP, by showing that Karp's approach to reduction generalizes to a specific type of approximability reduction..
P vs. NP NP-complete co-NP NP-hard
ProblГЁme NP-complet — WikipГ©dia. Adiabatic quantum optimization fails for random instances of NP-complete problems Boris Altshuler,1,2, Hari Krovi, 2,yand Jeremie Roland z 1Columbia University 2NEC Laboratories America Inc https://en.wikipedia.org/wiki/Nursing NP problems have their own significance in programming, but the discussion becomes quite hot when we deal with differences between NP, P , NP-Complete and NP-hard. P and NP- Many of us know the difference between them. P- Polynomial time solving. Problems ….
P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for NP-Complete: can be solved in Polynomial time only using a Non-deterministic method. NP-Complete may not last. Oh, one more thing, it is believed that if anyone could *ever* solve an "NP-Complete" problem in "P" time, then *all* "NP-complete" problems could also be solved that way by using the same method, and the whole class of "NP-Complete
Do not reduce L to a known NP-complete problem. We already knew you could do this; every NP problems is reducible to any NP-complete problem! P NP NPC. So what other problems are NP-complete? An independent set in an undirected graph is a set of vertices that have no edges between them. The Independent Set Problem Given an undirected graph G and a natural number n, the independent set problem NP-complete problems are the hardest in NP: if any NP-complete problem is p-time solvable, then all problems in NP are p-time solvable How to formally compare easiness/hardness of problems? Reductions Reduce language L 1 to L 2 via function f: 1. Convert input x of L 1 to instance f(x) of L 2 2. Apply decision algorithm for L 2 to f(x) Running time = time to compute f + time to apply decision
A Some NP-Complete Problems To ask the hard question is simple. But what does it mean? What are we going to do? W. H. Auden In this appendix we present a brief list of NP-complete problems; we restrict LECTURE NOTES: NP-COMPLETE PROBLEMS 3 checked in polynomial time. W is known as the ”witness” or ”certificate.” At worst, all solutions w must be checked, giving exponential running time.
List of PSPACE-complete problems. Jump to navigation Jump to search Here are some of the more commonly known problems that are PSPACE-complete when expressed as decision problems. This list is in no way comprehensive. The Partition-Knapsack Problem This problem is what we originally referred to as “knapsack.” Given a list of integers L, can we partition it into two disjoint sets whose sums are equal? Example: L={3,4,5,6,14,18}, Solution: 3+4+18=5+6+16 Partition-Knapsack is NP-complete; reduction from Knapsack.
Optimization Problems NP-complete problems are always yes/no questions. In practice, we tend to want to solve optimization problems, where our task is to minimize (or maximize) a … Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness.
22/08/2013 · NP-complete problems are the hardest problems in NP set. A decision problem L is NP-complete if: 1) L is in NP (Any given solution for NP-complete problems can be verified quickly, but there is no efficient known solution). 2) Every problem in NP … P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for
Since the original results, thousands of other problems have been shown to be NP-complete by reductions from other problems previously shown to be NP-complete; many of these problems are collected in Garey and Johnson's 1979 book Computers and Intractability: A Guide to the Theory of NP-Completeness. NP-complete Problems and Physical Reality Scott Aaronson∗ Abstract Can NP-complete problems be solved efficiently in the physical universe? I survey proposals including soap bubbles, protein folding, quantum computing, quantum advice, quantum adia-batic algorithms, quantum-mechanical nonlinearities, hidden variables, relativistic time dilation,
NP-complete special cases include the edge dominating set problem, i.e., the dominating set problem in line graphs. NP-complete variants include the connected dominating set problem and the maximum leaf spanning tree problem. 4 NP –HARD AND NP –COMPLETE PROBLEMS BASIC CONCEPTS •The computing times of algorithms fall into two groups. •Group1–consists of problems whose solutions are bounded by …
NP-complete problems are the hardest in NP: if any NP-complete problem is p-time solvable, then all problems in NP are p-time solvable How to formally compare easiness/hardness of problems? Reductions Reduce language L 1 to L 2 via function f: 1. Convert input x of L 1 to instance f(x) of L 2 2. Apply decision algorithm for L 2 to f(x) Running time = time to compute f + time to apply decision 16 NP-Hard Problems (December 3 and 5) 16.1 ‘E cient’ Problems A long time ago1, theoretical computer scientists like Steve Cook and Dick Karp decided that a minimum requirement of any e cient algorithm is that it runs in polynomial time: O(nc) for some constant c. People recognized early on that not all problems can be solved this quickly
However, David Zuckerman showed in 1996 that every one of these 21 problems has a constrained optimization version that is impossible to approximate within any constant factor unless P = NP, by showing that Karp's approach to reduction generalizes to a specific type of approximability reduction. NP-complete special cases include the edge dominating set problem, i.e., the dominating set problem in line graphs. NP-complete variants include the connected dominating set problem and the maximum leaf spanning tree problem.
P (Polynomial time decidable problems) is a class of problems which can be decided in polynomial time i.e., there's an algorithm for such a problem which tells whether the solution of a given instance of a problem is true/false in O(n^k) time for NP problems have their own significance in programming, but the discussion becomes quite hot when we deal with differences between NP, P , NP-Complete and NP-hard. P and NP- Many of us know the difference between them. P- Polynomial time solving. Problems …


